HA4 Task 3 - Geometric Theory

What are the fundamental principles behind the creation of virtual 3D space? Describe and explain 3D geometry.

Remember that you are trying to comprehensively explain the theory and applications of 3D with elucidated examples and consistently using subject terminology correctly.

In the broadest definition of the term, 3D would describe any object that occurs on a three-axis (3 dimensional)  Cartesian coordinate system.

A Cartesian coordinate system is basically a fancy way of describing the X, Y and Z axes with the X axis being horizontal, the Y axis being vertical and the Z axis being depth.

 

Geometric Theory and Polygons

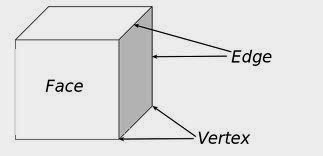
In Mesh modeling the basic object used is a vertex which is a point in three dimensional space. When two vertices are connected by a straight line it becomes an edge. When three vertices are connected to each other by three edges it creates a triangle which is the simplest polygon in Euclidean space. More complex polygons can be created out of multiple triangles, or as a single object with more than 3 vertices. Four sided polygons (generally referred to as quads) and triangles are the most common shapes used in polygonal modeling. A group of polygons, connected to each other by shared vertices, is generally referred to as an element. Each of the polygons making up an element is called a face.

In Euclidean geometry, any three non-collinear points determine a plane. For this reason, triangles always inhabit a single plane. This is not necessarily true of more complex polygons, however.

 

 

 

 
 
 
 
 
 

The flat nature of triangles makes it simple to determine their surface normal, a three-dimensional vector perpendicular to the triangle's surface. Surface normals are useful for determining light transport in ray tracing.

A group of polygons which are connected by shared vertices

is referred to as a mesh, often referred to as a wire frame model.

Information:  http://en.wikipedia.org/wiki/Polygonal_modelling

 Primitives:

Primitives are the building blocks of 3D—basic geometric forms that you can use as is or modify with transforms and Booleans. Although it's possible to create most of these objects by lathing or extruding 2D shapes, most software packages build them in for speed and convenience.


 











The most common 3D primitives are cubes, pyramids, cones, spheres, and tori. Like 2D shapes, these primitives can have a resolution level assigned to them so that you can make them look smoother by boosting the number of sides and steps used to define them.

Information: http://www.peachpit.com/articles/article.aspx?p=30594&seqNum=5

Surfaces:

Polygonal models must be defined as specific surfaces to add colours and texture to the surface and it must be given a skeleton for animation. Meshes can also be assigned weights and centre of gravity for use in physical simulation.

 

Information:

http://en.wikipedia.org/wiki/Polygonal_modelling